23. When the wickets fall
Over the years there's a remarkable consistency to when ODI teams have lost wickets
A popular mathematical technique when analysing highly dynamic and fast-changing systems is to look for things that don’t change. We can call them “invariants”. There is a whole class of theorems distributed through different areas of mathematics that are known as “fixed point theorems”. My favourite among them comes from Topology, where there is a rather fantastically named theorem called “Hairy Ball Theorem”.
There is no doubt that one day international cricket has changed significantly in the last three decades. Scoring rates have gone up significantly. The way teams build an innings seems to have changed. Rules change every couple of years. A substitute came in for a couple of years and then went out. One day specialists came in. And then there were bits and pieces players. Batting strategies and bowling strategies changed.
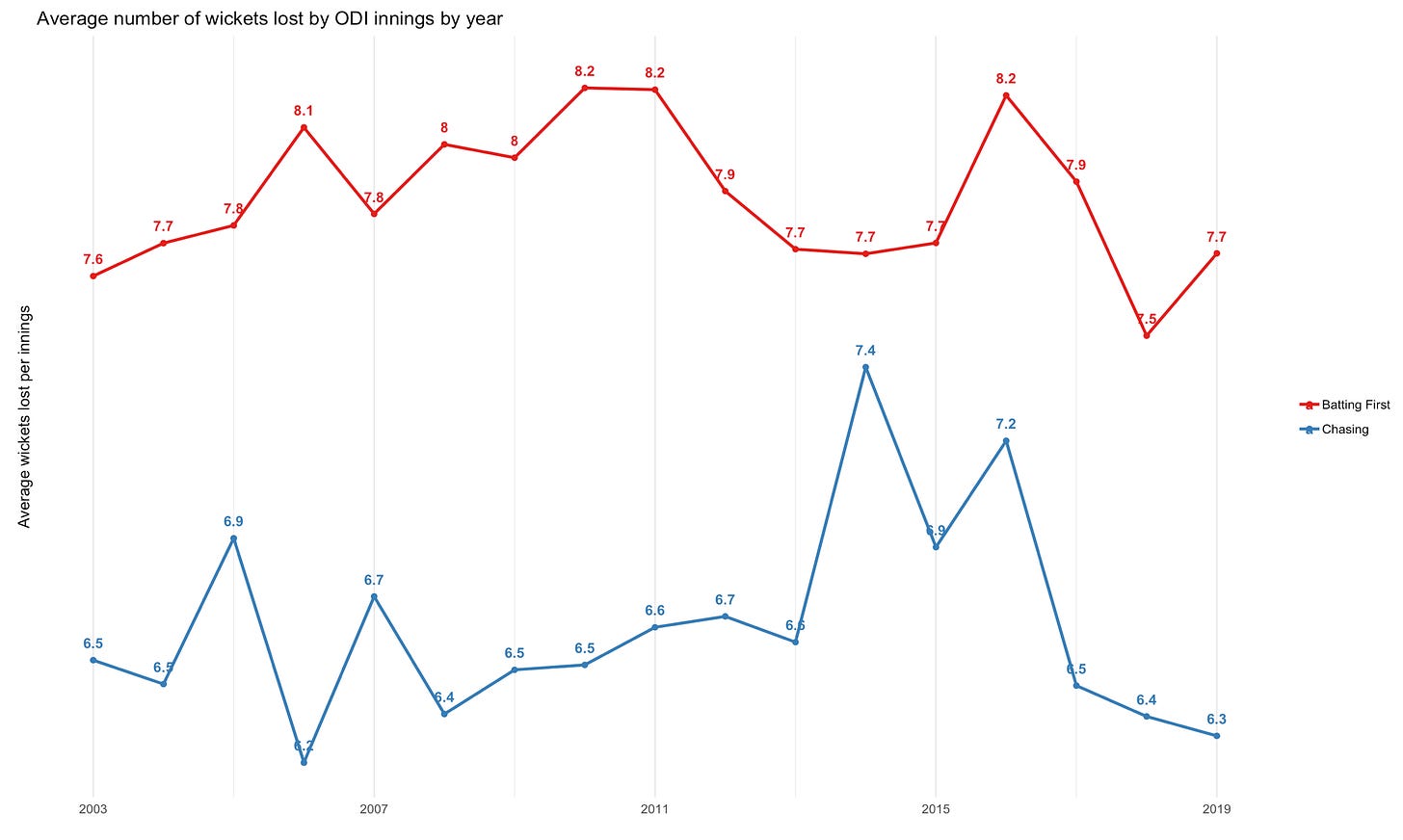
Among all this one thing has been rather remarkably consistent across the years - the fall of wickets. Whether we look at the fall of wickets based on the score at which the wicket falls, or the time of innings when it falls, there has been remarkably little change over the years (though this decade we see that wickets are falling slightly later).

The first wicket falls for 35 at the end of the seventh over. The second for 69 after fourteen overs. The third for 103 after 21 overs (isn’t it interesting that wickets fall “at regular intervals” in the beginning of the innings?). And then, on average, wickets fall faster, with teams going to 134/4 in 28 overs, 158/5 in 33 and 175/6 in 37. The data to produce this includes all ODIs from 1998 onwards (which is when we started really keeping records of when the wickets fall, rather than just the score at which the wickets fall).

That wickets four to six fall at faster intervals might be down to selection bias inherent in the data - when we look at the average score of when the fourth wicket falls, we only consider those innings where four of more wickets have fallen. Innings where three or fewer wickets were lost are ignored. Yet, what matters here is that the graphs above are largely flat - despite massive changes in strategies and rules and personnel and all that.
My hypothesis when I started this analysis is that wickets must be falling sooner (at least in terms of overs) because teams are taking greater risk. As time has passed, teams have appreciated that the amount of resource available in terms of number of overs is limited, and so the price of a wicket (relative to balls remaining) is actually lower, which has resulted in greater risk taking - this was my hypothesis. It doesn’t seem to be true.
In other words, the increase in the scores in ODI cricket doesn’t seem to be on account of greater risk taking. Had teams been taking greater risk, this would have meant wickets falling earlier and teams losing more wickets at the end of their innings. However, the number of wickets lost at the end of the first innings has been fairly constant over time.
Now that my hypothesis has been disproven, I wonder why teams aren’t taking higher risk. If you have any good ideas, please let me know.

